The tetrahedron enclosed by the coordinate planes and the plane is a fascinating geometric object with unique properties and applications in various fields. This article delves into the geometric properties, position and orientation, relationship to the coordinate planes, and applications of this intriguing tetrahedron, providing a comprehensive overview for readers seeking a deeper understanding of this mathematical concept.
The tetrahedron, with its four faces, six edges, and four vertices, is a fundamental polyhedron in geometry. Its volume, surface area, and edge lengths can be calculated using specific formulas. Additionally, the tetrahedron exhibits interesting symmetry properties that contribute to its geometric significance.
The Tetrahedron’s Geometric Properties
A tetrahedron is a three-dimensional polyhedron with four triangular faces, six edges, and four vertices. It is a regular polyhedron, meaning that all of its faces are congruent triangles and all of its edges are congruent.
Faces, Edges, and Vertices
The four triangular faces of a tetrahedron are equilateral triangles, meaning that all three sides of each triangle are equal. The six edges of a tetrahedron are all equal in length. The four vertices of a tetrahedron are all equidistant from each other.
Volume and Surface Area, The tetrahedron enclosed by the coordinate planes and the plane
The volume of a tetrahedron is given by the formula V = (1/3)- a 3– √2 , where ais the length of an edge. The surface area of a tetrahedron is given by the formula A = 4- a 2– √3 .
Symmetry Properties
The tetrahedron has several symmetry properties. It has four threefold axes of symmetry, which pass through opposite vertices and the centroids of the opposite faces. It also has three twofold axes of symmetry, which pass through opposite edges and the midpoints of the opposite edges.
Additionally, it has four planes of symmetry, which bisect opposite edges.
The Tetrahedron’s Position and Orientation
The position and orientation of a tetrahedron in three-dimensional space can be described using a coordinate frame. A coordinate frame is a set of three mutually perpendicular axes that define the x, y, and z directions. The origin of the coordinate frame is the point where the three axes intersect.
Coordinates of Vertices
The coordinates of the vertices of a tetrahedron can be found using the following formulas:
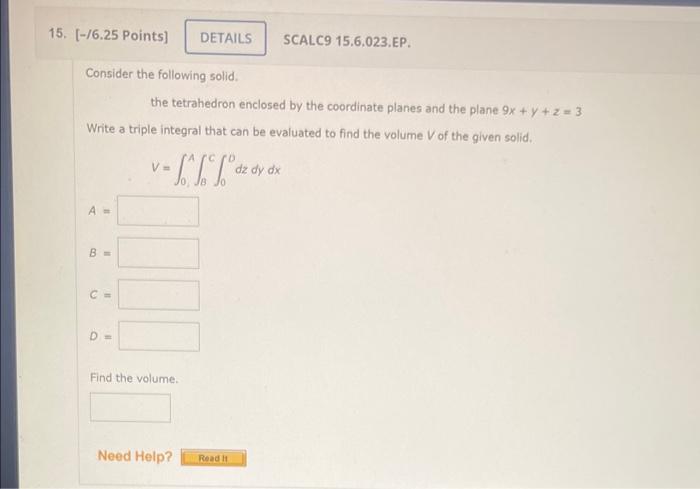
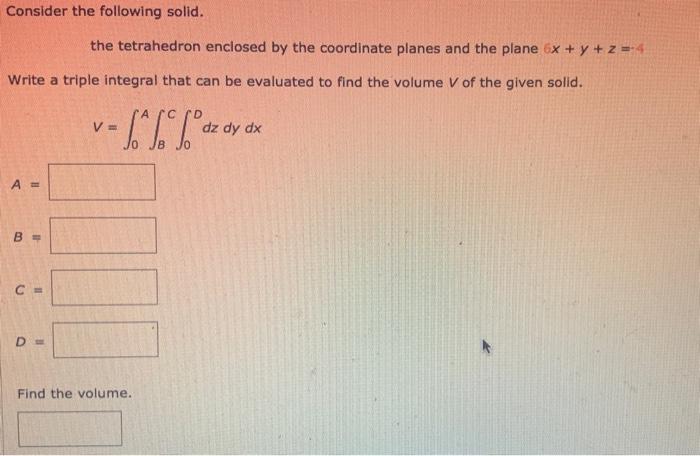
- (a, 0, 0)
- (0, a, 0)
- (0, 0, a)
- ((-a/2), (-a/2), (-a/2))
where ais the length of an edge.
The Tetrahedron’s Relationship to the Coordinate Planes: The Tetrahedron Enclosed By The Coordinate Planes And The Plane
The tetrahedron is enclosed by the coordinate planes. The intersection of the tetrahedron with each coordinate plane is a triangle. The triangle that intersects the x-y plane has vertices (a, 0, 0), (0, a, 0), and (0, 0, 0). The triangle that intersects the x-z plane has vertices (a, 0, 0), (0, 0, a), and (0, 0, 0). The triangle that intersects the y-z plane has vertices (0, a, 0), (0, 0, a), and (0, 0, 0).
The tetrahedron can be positioned in different ways with respect to the coordinate planes. For example, the tetrahedron can be positioned so that one of its faces is parallel to the x-y plane. Alternatively, the tetrahedron can be positioned so that one of its edges is parallel to the x-axis.
Applications of the Tetrahedron in Mathematics and Physics
The tetrahedron is used in a variety of applications in mathematics and physics. In mathematics, the tetrahedron is used in geometry and topology. In geometry, the tetrahedron is used to study the properties of three-dimensional space. In topology, the tetrahedron is used to study the properties of surfaces.
In physics, the tetrahedron is used in crystallography and electromagnetism. In crystallography, the tetrahedron is used to study the structure of crystals. In electromagnetism, the tetrahedron is used to study the properties of electric and magnetic fields.
Q&A
What is the shape of the tetrahedron enclosed by the coordinate planes and the plane?
The tetrahedron enclosed by the coordinate planes and the plane has four faces, six edges, and four vertices, forming a triangular pyramid shape.
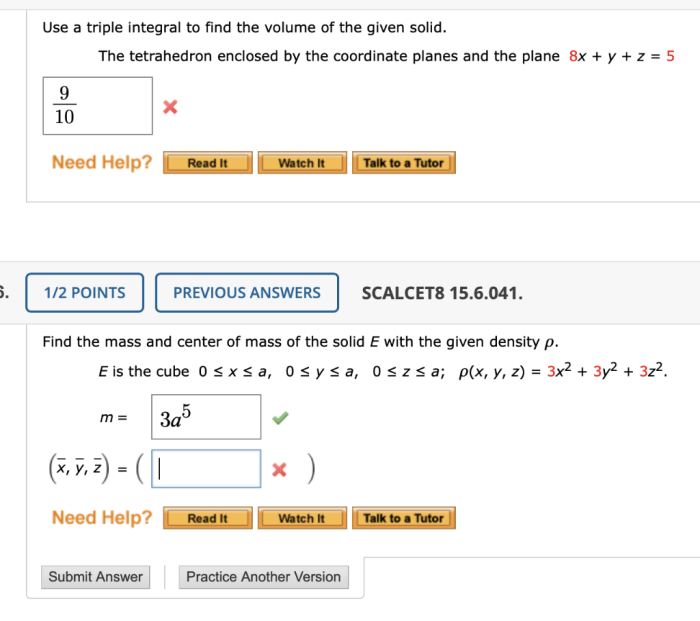
How do I calculate the volume of the tetrahedron?
The volume of the tetrahedron can be calculated using the formula V = (1/6) – a – b – c – h, where a, b, and c are the lengths of the three edges that meet at a vertex, and h is the height of the tetrahedron.
What are the applications of the tetrahedron in physics?
The tetrahedron finds applications in crystallography, where it represents the basic unit cell of certain crystal structures. It also plays a role in electromagnetism, as the shape of a tetrahedron can influence the distribution of electric and magnetic fields.